Phase transition models with hysteresis
Most materials in slPCMlib database have different heat capacity data for heating and cooling. These PCM show thermal hysteresis in the phase change. The following models are considered to account for thermal hysteresis:
- curve track hysteresis model
- curve switch hysteresis model
- curve scale hysteresis model
The models are included in the Modelica/Dymola library GitHub-slPCMlib.
Examples
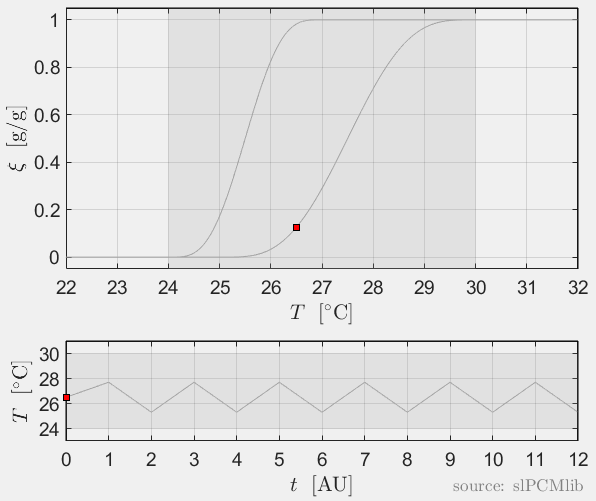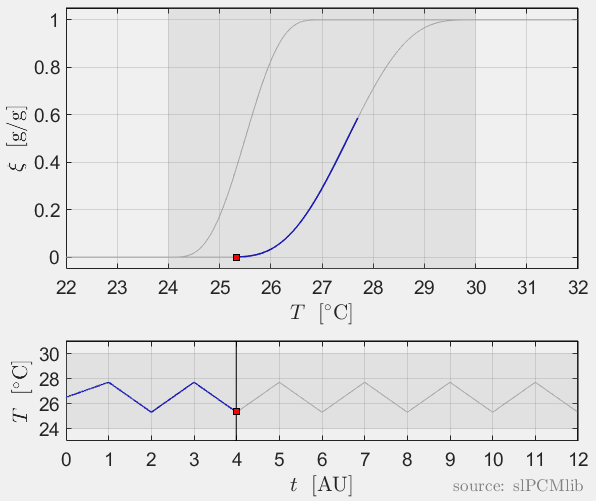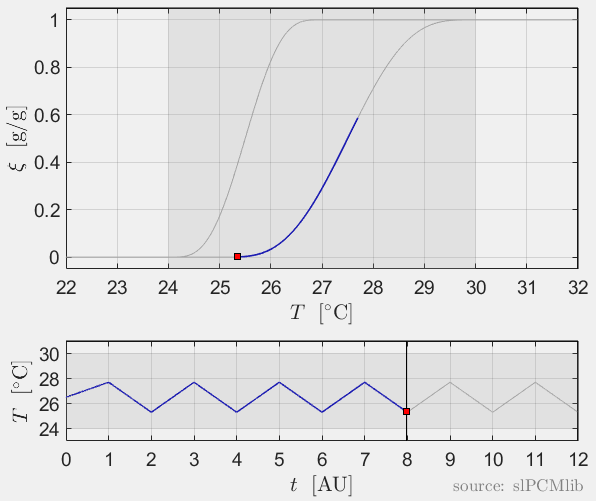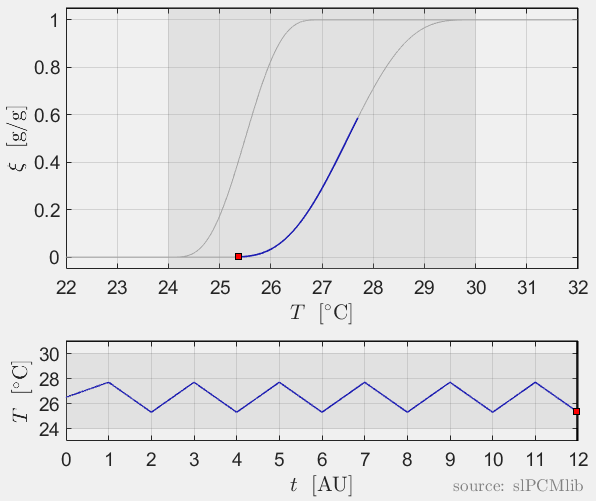
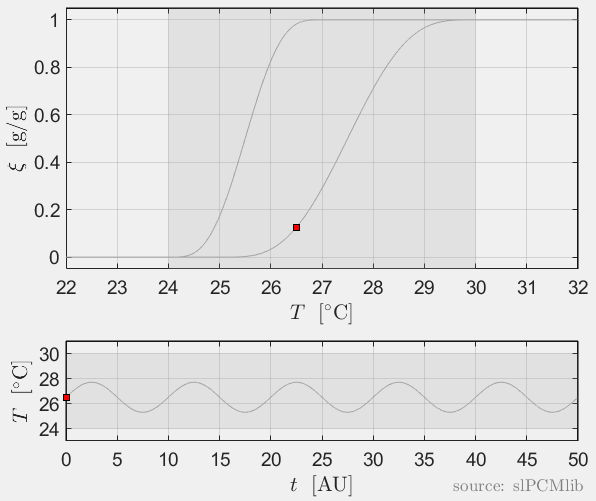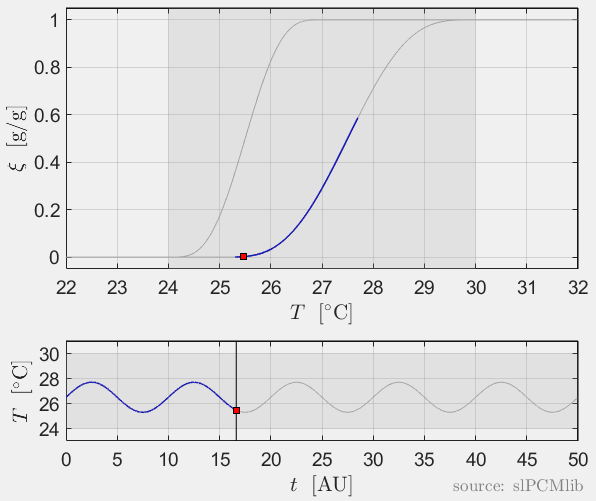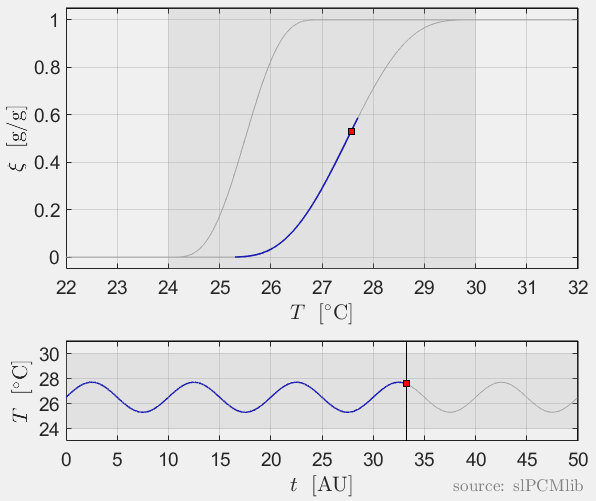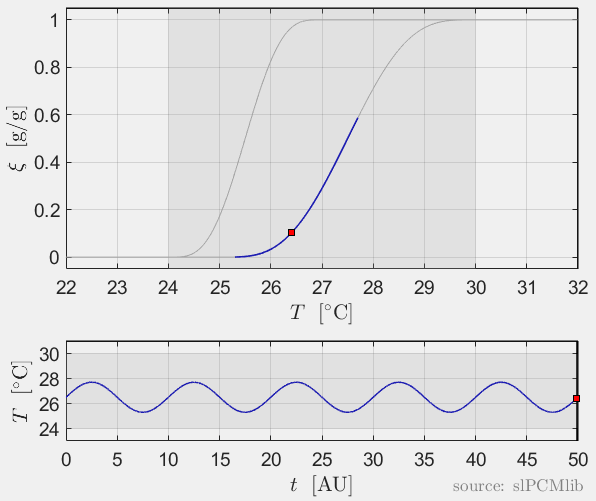
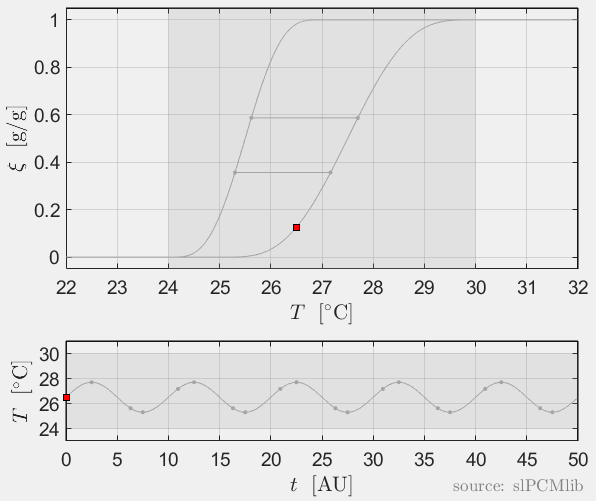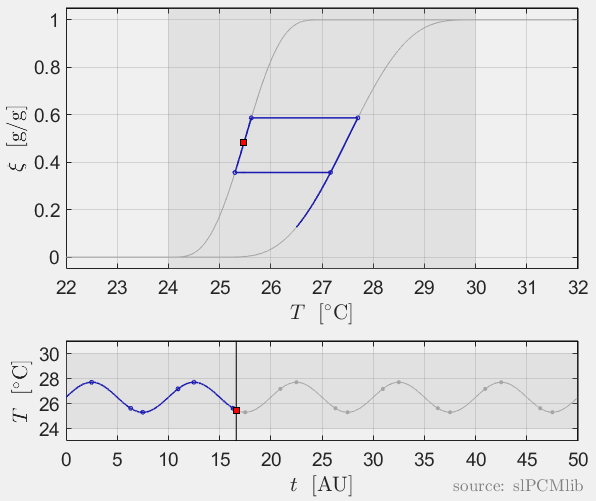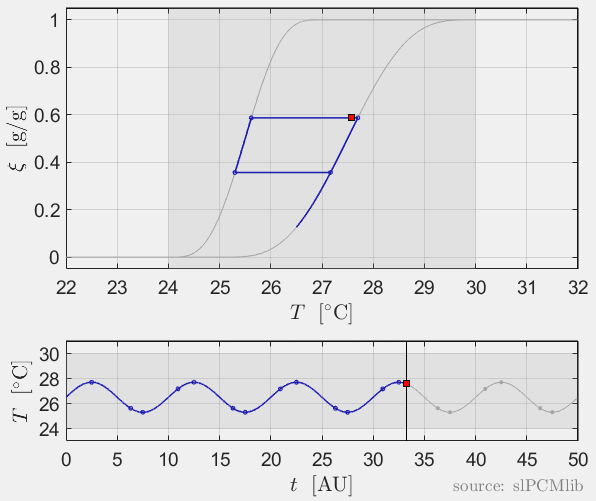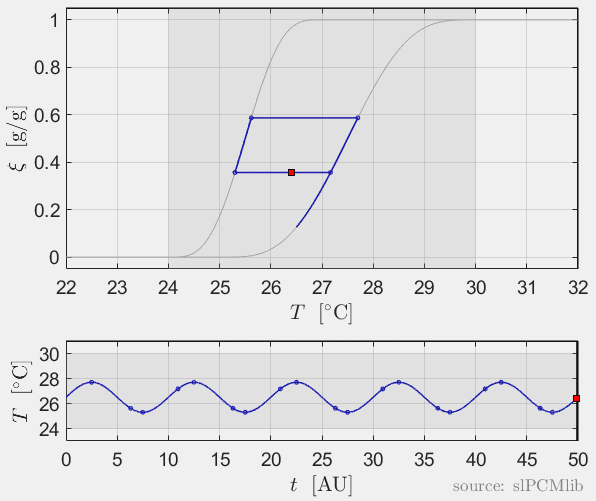
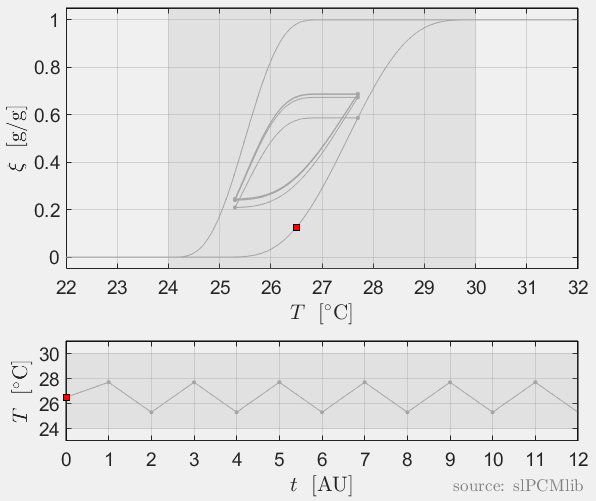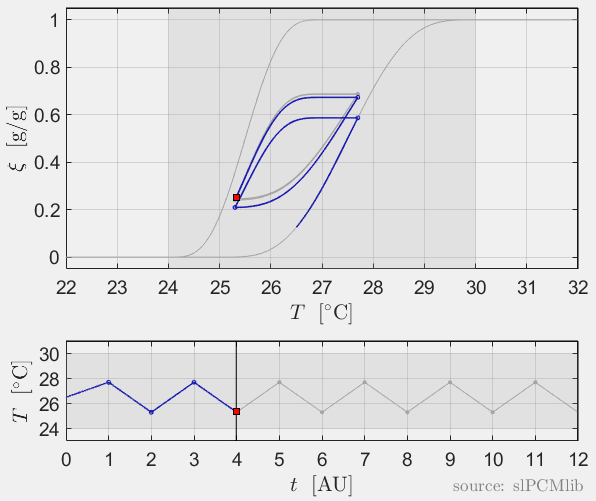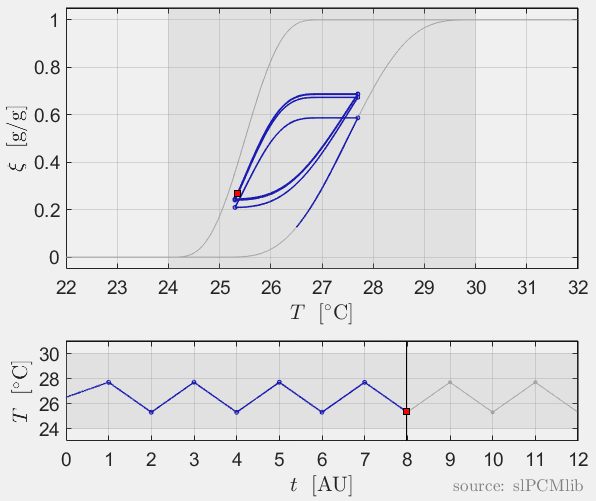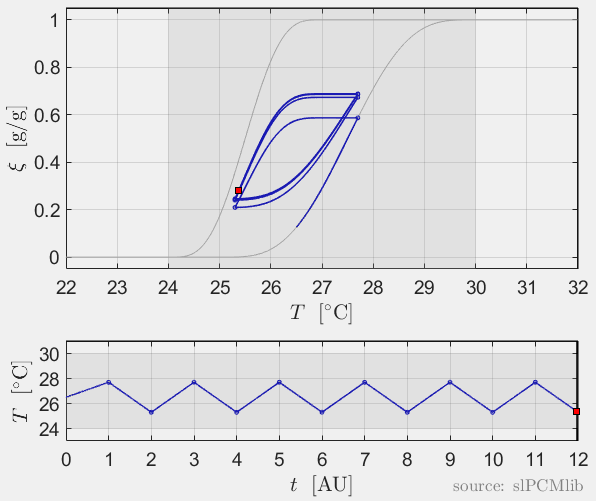
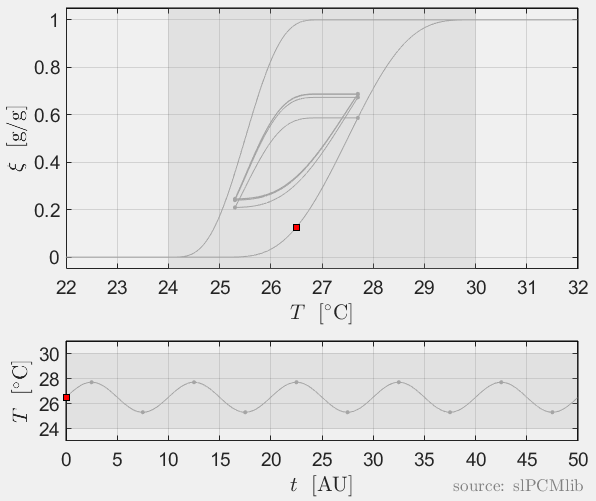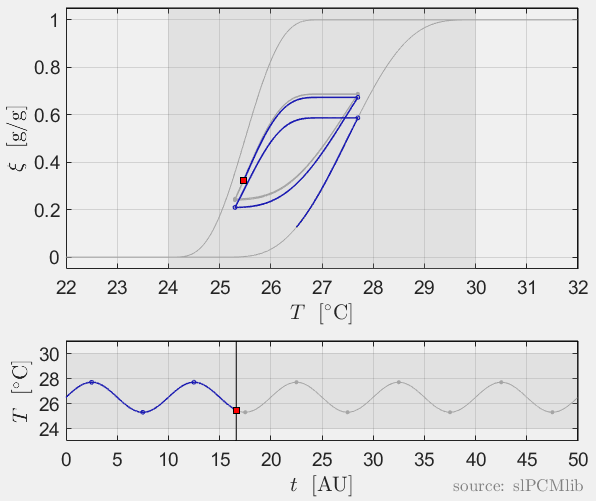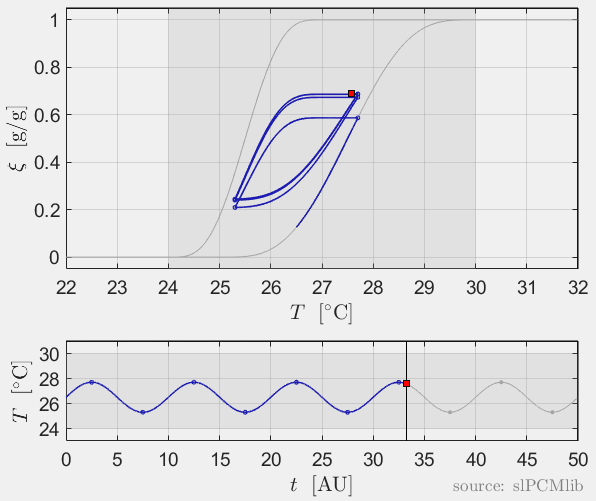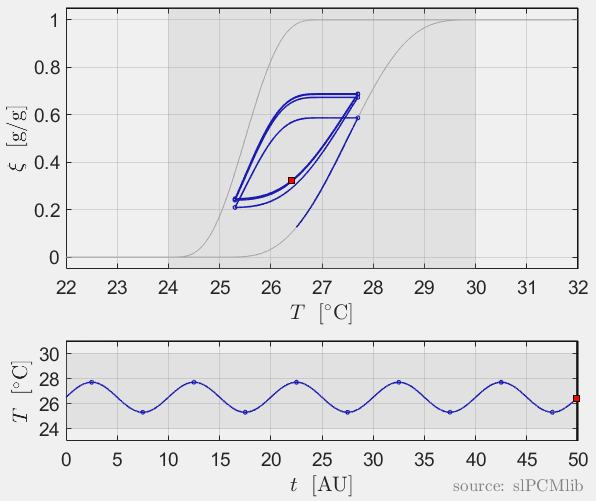
Interrupted melting and solidification
The predicted phase fractions are very different for hysteresis each model. It is obvious, that that the curve track model is not able to reproduce hysteresis for interupted/ incomplete phase change processes, see below.
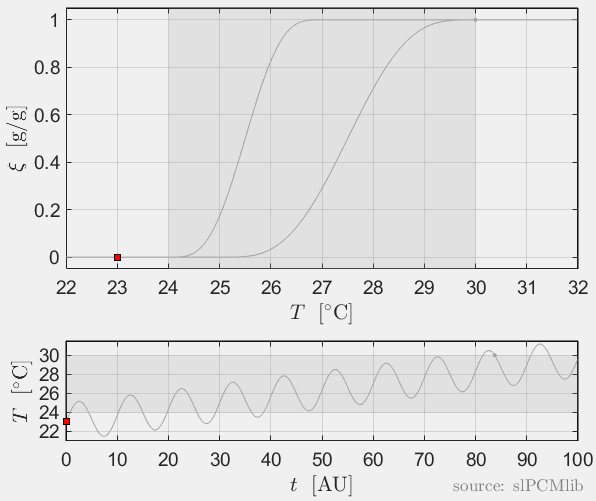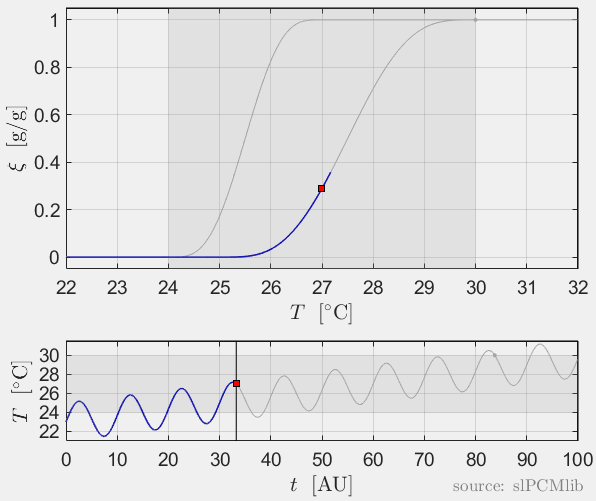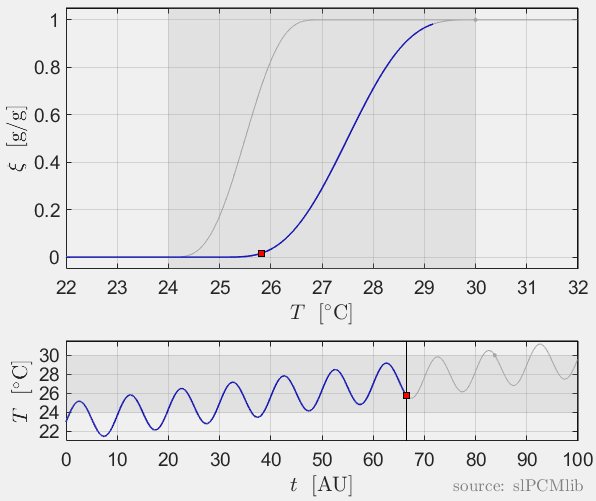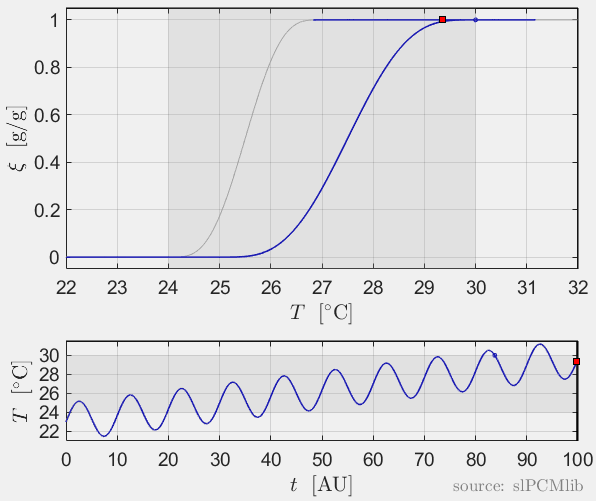
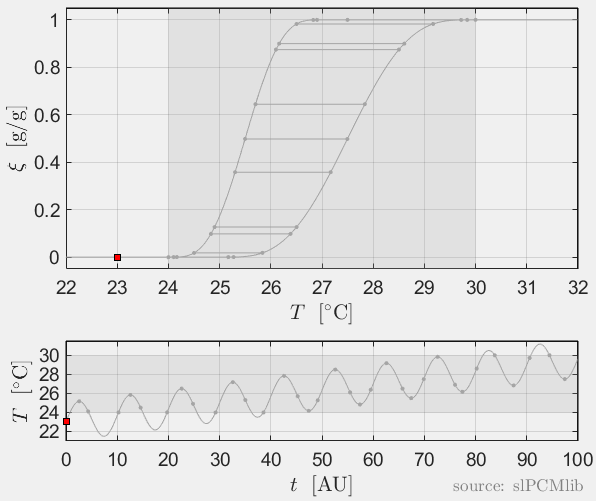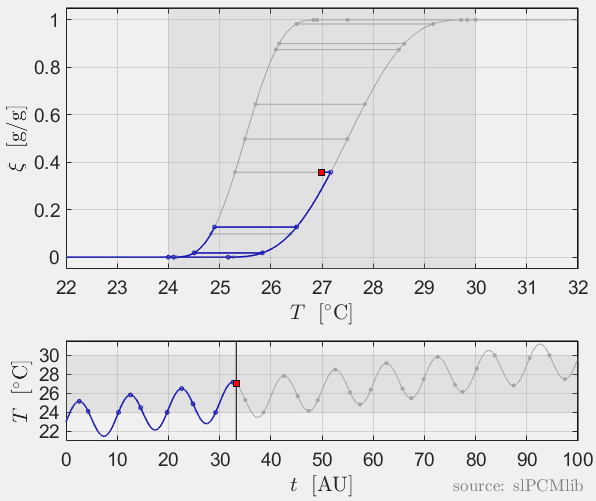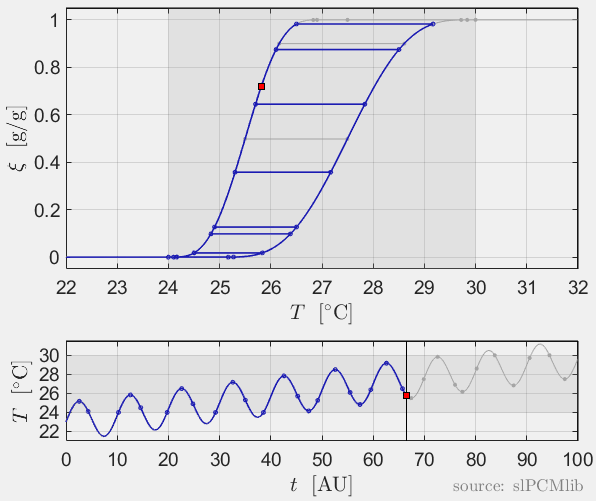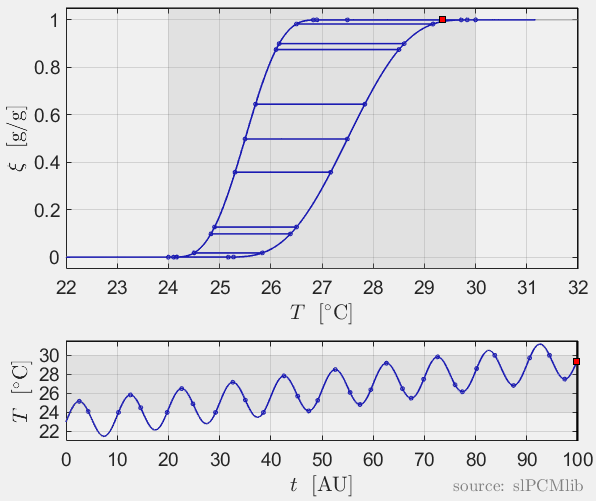
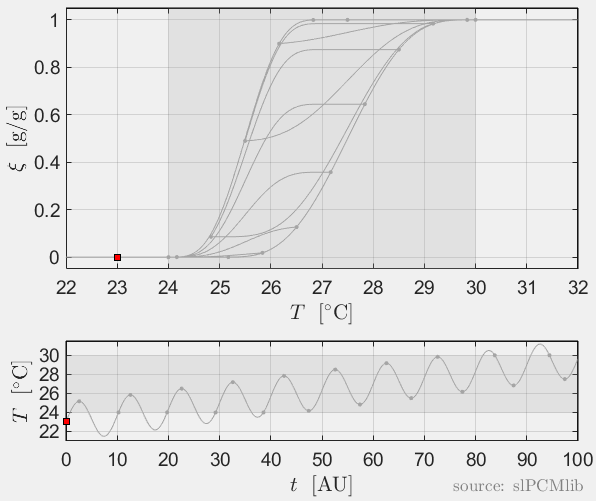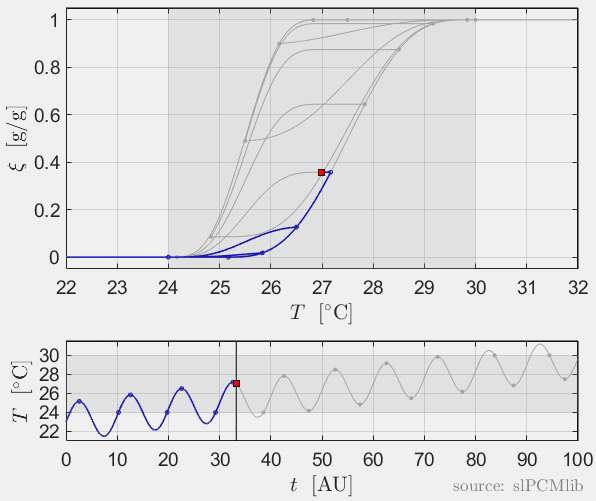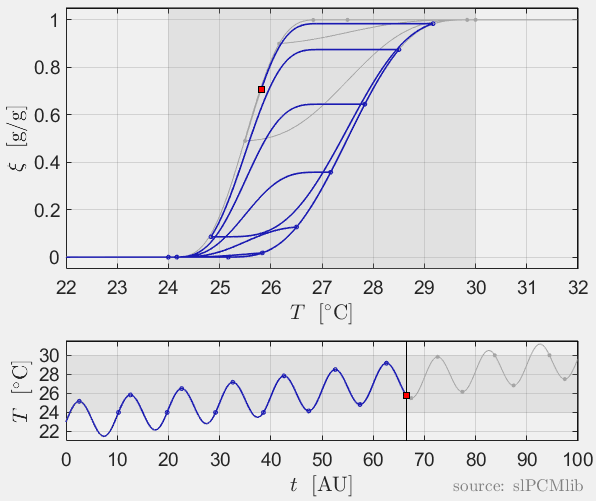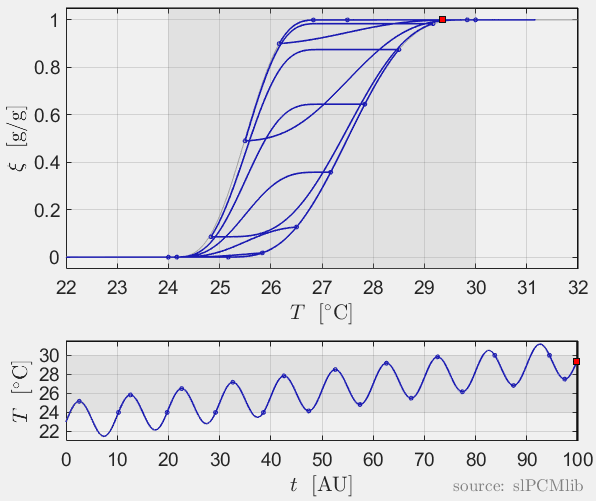
Rate-independence
All models are rate-independent: increased heating rates lead to faster melting but result in the same state (phase fraction) for any stopping temperature. Accordingly, also the magnitude of the hysteresis is rate-independent, compare left and right plots.
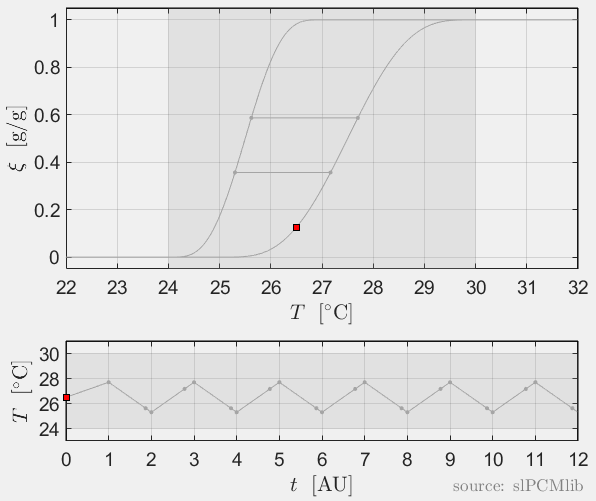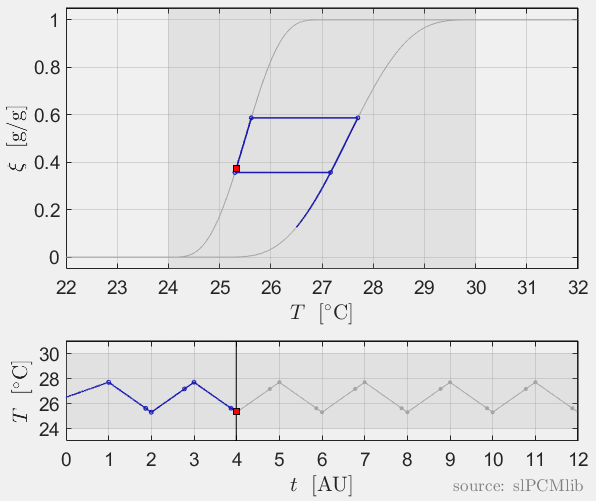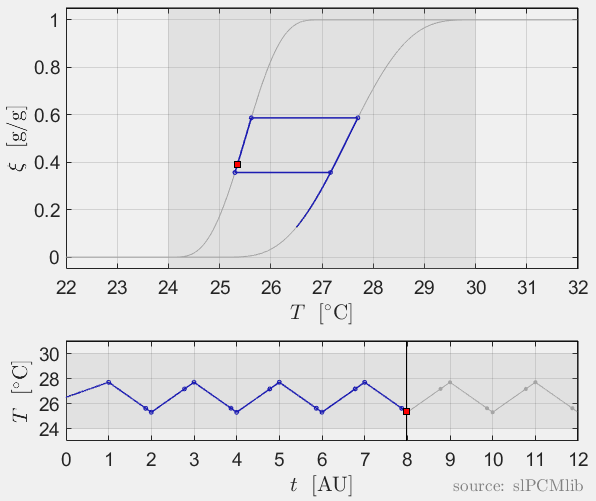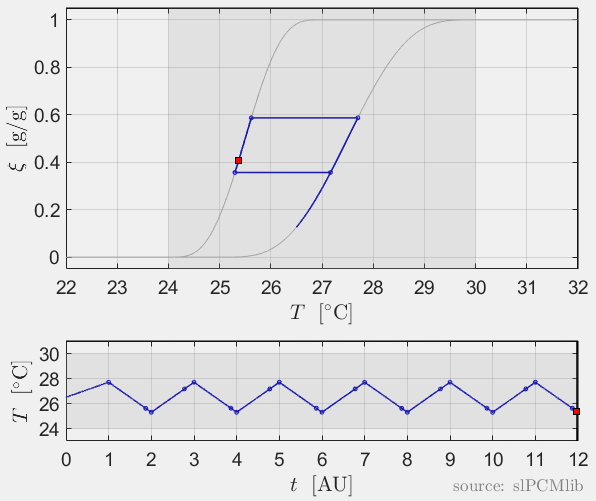
Heat conduction in PCM
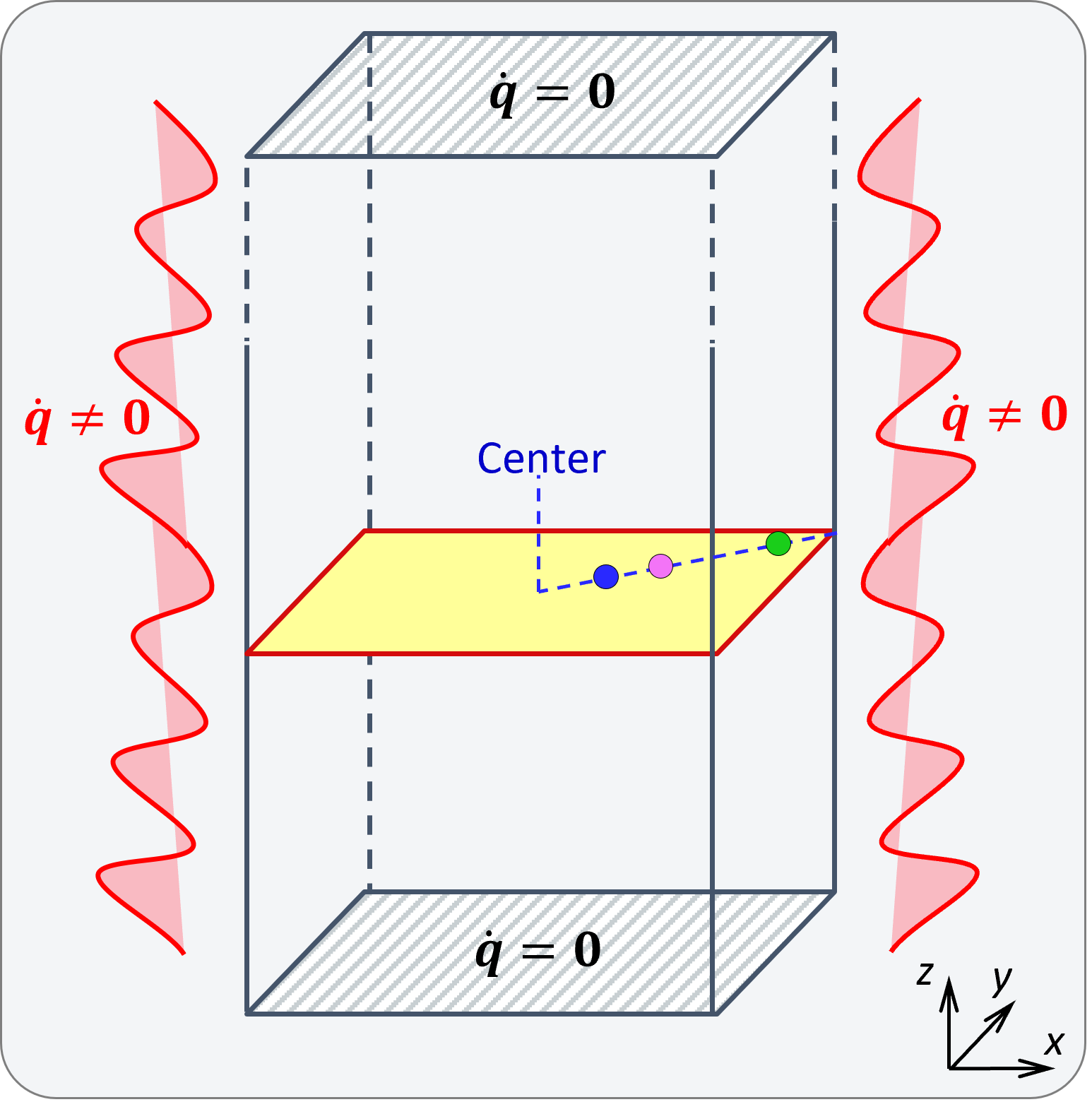
This example considers heat conduction in PCM on a rectangular 2D (x,y) domain. A perfect temperature control is assumed at the boundaries of the domain and a sinusoidal excitation signal. For the numerical solution the heat conduction equation is discretized. For each grid point a discrete heat conduction equation and a (curve scale) hysteresis model are solved. Computed phase fractions and enthalpies are highligthed for three grid points (green, magenta, blue).
References
- Barz, T., Emhofer, J., Marx, K., Zsembinszki, G., & Cabeza, L. F. (2019).
Phenomenological modelling of phase transitions with hysteresis in solid/liquid PCM.
Journal of Building Performance Simulation, 12(6), 770-788. DOI: https://doi.org/10.1080/19401493.2019.1657953 - Barz, T. (2021).
Paraffins as phase change material in a compact plate-fin heat exchanger-Part II: Validation of the “curve scale” hysteresis model for incomplete phase transitions.
Journal of Energy Storage, 34, 102164. DOI: https://doi.org/10.1016/j.est.2020.102164